dot-calculus

pDOT Type Safety Proof

This repository contains the Coq formalization type-safety proof of the pDOT calculus that generalizes DOT by Amin et al. (2016). with paths of arbitrary length. This allows us to express path-dependent types of the form x.a.b.A as opposed to just x.A.

pDOT paper | Github repo

Compiling the Proof

System requirements:

 opam repo add coq-released http://coq.inria.fr/opam/released
 opam install -j4 coq-tlc

To compile the proof, run

 git clone https://github.com/amaurremi/dot-calculus.git
 cd src/extensions/paths
 make

Overview

This repository formalizes the type-safety proof of the pDOT calculus as presented in our paper. Specifically, it defines the calculus itself (its abstract syntax (paper, Coq), type system (paper, Coq), and operational semantics (paper, Coq)). The Type Soundness Theorem (paper, Coq) proves that well-typed terms in pDOT either diverge (i.e. run forever) or reduce to a normal form, which includes values (functions and objects) or paths. Since the operational semantics does not reduce paths we present an Extended Type Soundness Theorem (paper, Coq) defined in terms of the above reduction relation extended with the lookup operation (paper, Coq) that looks up paths in the runtime environment. This theorem states that a well-typed term either diverges or reduces to a value (which does not include paths).

Paper Correspondence

The pDOT calculus is formalized using the locally nameless representation with cofinite quantification in which free variables are represented as named variables, and bound variables are represented as de Bruijn indices.

We include the Sequences library by Xavier Leroy into our development to reason about the reflexive, transitive closure of binary relations.

Correspondence of Definitions

Definition In paper File Paper notations Proof notations Name in proof
Abstract Syntax Fig. 1 Definitions.v      
- variable Fig. 1 Definitions.v     avar
- term member Fig. 1 Definitions.v     trm_label
- type member Fig. 1 Definitions.v     typ_label
- path Fig. 1 Definitions.v x.a.b.c

p.a

p.b̅		 p_sel x (c::b::a::nil)

p•a

p••b		 path
- term Fig. 1 Definitions.v     trm
- stable term Fig. 1 Definitions.v     def_rhs
- value Fig. 1 Definitions.v ν(x: T)ds
λ(x: T)t		 ν(T)ds
λ(T)t		 val
- definition Fig. 1 Definitions.v {a = t}
{A = T}		 {a := t}
{A ⦂= T}		 def
- type Fig. 1 Definitions.v {a: T}
{A: T..U}
∀(x: T)U
p.A
p.type
μ(x: T)
T ∧ U
⊤
⊥		 {a ⦂ T}
{A >: T <: U}
∀(T)U
p↓A
{{p}}
μ(T)
T ∧ U
⊤
⊥		 typ
Type System Fig. 2 Definitions.v      
- term typing Fig. 2 Definitions.v Γ ⊢ t: T Γ ⊢ t : T ty_trm
- replacement operation<a href=#simplified-replacement-definition>*</a> Fig. 9 Definitions.v T[q/p]=U (replacing path p with q in T yields U) repl_typ p q T U ty_trm
- definition typing Fig. 2 Definitions.v p; Γ ⊢ d: T x; bs; Γ ⊢ d : T
(single definition)
x; bs; Γ ⊢ d :: T
(multiple definitions)
Here, p=x.bs, i.e. x
is p’s receiver, and
bs are p’s fields
in reverse order		 ty_def
ty_defs
- tight bounds Fig. 2 Definitions.v     tight_bounds
- subtyping Fig. 2 Definitions.v Γ ⊢ T <: U Γ ⊢ T <: U subtyp
Operational semantics Fig. 3 Reduction.v γ|t ⟼ γ’|t’
γ|t ⟼* γ’|t’		 (γ, t) ⟼ (γ', t')
(γ, t) ⟼* (γ', t')		 red
Path lookup Fig. 4 Lookup.v γ ⊢ p ⤳ s
γ ⊢ s ⤳* s’		 γ ⟦ p ⤳ s ⟧
γ ⟦ s ⤳* s' ⟧		 lookup_step
Extended reduction Sec. 5 Safety.v γ|t ↠ γ’|t’
γ|t ↠* γ’|t’		 (γ, t) ↠ (γ', t')
(γ, t) ↠* (γ', t')		 extended_red
Inert and record types Fig. 5 Definitions.v inert T
inert Γ		   inert_typ
inert
Well-formed
environments		 Sec. 5.2.1 PreciseTyping.v     wf
Correspondence
between a value
and type environment		 Sec. 5 Definitions.v γ: Γ γ ⫶ Γ well_typed

Simplified Replacement Definition

The presented definition of replacement excludes the index n which, in the submitted version of the paper, indicated precisely which occurrence of a path p in a type T should be replaced with q. More specifically, in the submitted version of the paper, the replacement operation was defined as T[q/p,n] which states that

We simplified the definition of replacement by generalizing it so that it is not tied to a specific index n. The new definition of replacement is T[q/p] which indicates that some occurrence of p in T is replaced with q. The final version of the paper, which we include in the artifact, presents this simplified replacement operation.

Correspondence of Lemmas and Theorems

Theorem File Name in proof
Theorem 5.1 (Soundness) Safety.v safety
Theorem 5.2 (Extended Soundness) Safety.v extended_safety
Lemma 5.3 (Progress) Safety.v progress
Lemma 5.4 (Preservation) Safety.v preservation
Lemma 5.5 CanonicalForms.v canonical_forms_fun

Correspondence of Examples

Example In paper File
List example Figure 6 a ListExample.v
Compiler example Figure 6 b CompilerExample.v
Singleton type example Figure 6 c SingletonTypeExample.v

Proof Organization

Safety Proof

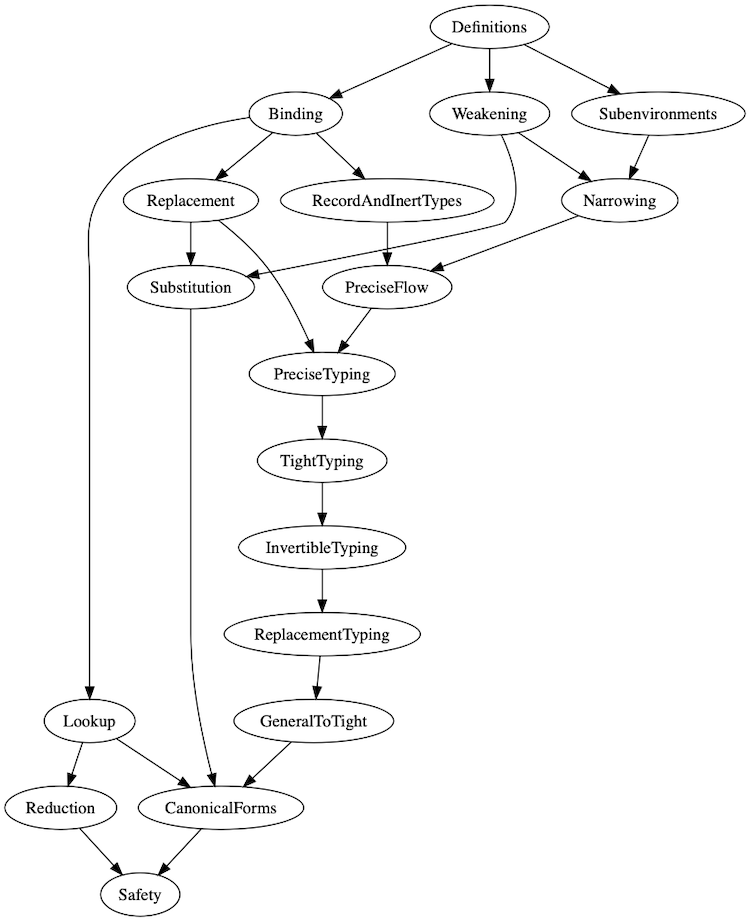
The Coq proof is split up into the following modules:

Examples

The following figure shows a dependency graph between the Coq modules:

Dependency graph